bamlss: A Lego toolbox for flexible Bayesian regression
Citation
Umlauf N, Klein N, Simon T, Zeileis A (2019). “bamlss: A Lego Toolbox for Flexible Bayesian Regression (and Beyond).” arXiv:1909.11784, arXiv.org E-Print Archive. https://arxiv.org/abs/1909.11784
Abstract
Over the last decades, the challenges in applied regression and in predictive modeling have been changing considerably: (1) More flexible model specifications are needed as big(ger) data become available, facilitated by more powerful computing infrastructure. (2) Full probabilistic modeling rather than predicting just means or expectations is crucial in many applications. (3) Interest in Bayesian inference has been increasing both as an appealing framework for regularizing or penalizing model estimation as well as a natural alternative to classical frequentist inference. However, while there has been a lot of research in all three areas, also leading to associated software packages, a modular software implementation that allows to easily combine all three aspects has not yet been available. For filling this gap, the R package bamlss is introduced for Bayesian additive models for location, scale, and shape (and beyond). At the core of the package are algorithms for highly-efficient Bayesian estimation and inference that can be applied to generalized additive models (GAMs) or generalized additive models for location, scale, and shape (GAMLSS), also known as distributional regression. However, its building blocks are designed as “Lego bricks” encompassing various distributions (exponential family, Cox, joint models, …), regression terms (linear, splines, random effects, tensor products, spatial fields, …), and estimators (MCMC, backfitting, gradient boosting, lasso, …). It is demonstrated how these can be easily recombined to make classical models more flexible or create new custom models for specific modeling challenges.
Software
CRAN package: https://CRAN.R-project.org/package=bamlss
Replication script: bamlss.R
Project web page: http://www.bamlss.org/
Quick overview
To illustrate that the bamlss follows the same familiar workflow of the other regression packages such as the basic stats package or the well-established mgcv or gamlss two quick examples are provided: a Bayesian logit model and a location-scale model where both mean and variance of a normal response depend on a smooth term.
The logit model is a basic labor force participation model, a standard application in microeconometrics. Here, the data are loaded from the AER package and the same model formula is specified that would also be used for glm() (as shown on ?SwissLabor).
data("SwissLabor", package = "AER")
f <- participation ~ income + age + education + youngkids + oldkids + foreign + I(age^2)
Then, the model can be estimated with bamlss() using essentially the same look-and-feel as for glm(). The default is to use Markov chain Monte Carlo after obtaining initial parameters via backfitting.
library("bamlss")
set.seed(123)
b <- bamlss(f, family = "binomial", data = SwissLabor)
summary(b)
## Call:
## bamlss(formula = f, family = "binomial", data = SwissLabor)
## ---
## Family: binomial
## Link function: pi = logit
## *---
## Formula pi:
## ---
## participation ~ income + age + education + youngkids + oldkids +
## foreign + I(age^2)
## -
## Parametric coefficients:
## Mean 2.5% 50% 97.5% parameters
## (Intercept) 6.15503 1.55586 5.99204 11.11051 6.196
## income -1.10565 -1.56986 -1.10784 -0.68652 -1.104
## age 3.45703 2.05897 3.44567 4.79139 3.437
## education 0.03354 -0.02175 0.03284 0.09223 0.033
## youngkids -1.17906 -1.51099 -1.17683 -0.83047 -1.186
## oldkids -0.24122 -0.41231 -0.24099 -0.08054 -0.241
## foreignyes 1.16749 0.76276 1.17035 1.55624 1.168
## I(age^2) -0.48990 -0.65660 -0.49205 -0.31968 -0.488
## alpha 0.87585 0.32301 0.99408 1.00000 NA
## ---
## Sampler summary:
## -
## DIC = 1033.325 logLik = -512.7258 pd = 7.8734
## runtime = 1.417
## ---
## Optimizer summary:
## -
## AICc = 1033.737 converged = 1 edf = 8
## logLik = -508.7851 logPost = -571.3986 nobs = 872
## runtime = 0.012
## ---
The summary is based on the MCMC samples, which suggest “significant” effects for all covariates, except for variable education, since the 95% credible interval contains zero. In addition, the acceptance probabilities alpha are reported and indicate proper behavior of the MCMC algorithm. The column parameters shows respective posterior mode estimates of the regression coefficients, which are calculated by the upstream backfitting algorithm.
To show a more flexible regression model we fit a distributional scale-location model to the well-known simulated motorcycle accident data, provided as mcycle in the MASS package.
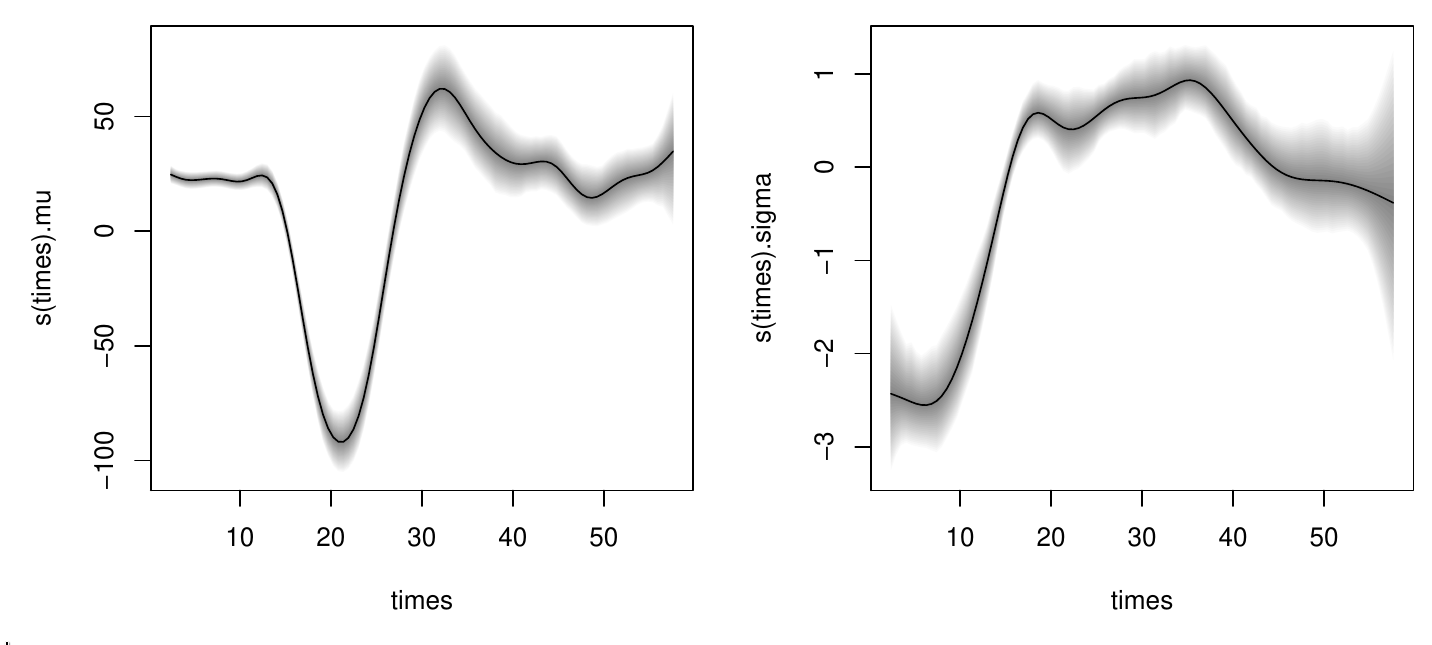
Here, the relationship between head acceleration and time after impact is captured by smooth relationships in both mean and variance. See also ?gaulss in the mgcv package for the same type of model estimated with REML rather than MCMC. Here, we load the data, set up a list of two formula with smooth terms (and increased knots k for more flexibility), fit the model almost as usual, and then visualize the fitted terms along with 95% credible intervals.
data("mcycle", package = "MASS")
f <- list(accel ~ s(times, k = 20), sigma ~ s(times, k = 20))
set.seed(456)
b <- bamlss(f, data = mcycle, family = "gaussian")
plot(b, model = c("mu", "sigma"))
Flexible count regression for lightning reanalysis
Finally, we show a more challenging case study. Here, emphasis is given to the illustration of the workflow. For more details on the background for the data and interpretation of the model, see Section 5 in the full paper linked above. The goal is to establish a probabilistic model linking positive counts of cloud-to-ground lightning discharges in the European Eastern Alps to atmospheric quantities from a reanalysis dataset.
The lightning measurements form the response variable and regressors are taken from the atmospheric quantities from ECMWF’s ERA5 reanalysis data. Both have a temporal resolution of 1 hour for the years 2010-2018 and a spatial mesh size of approximately 32 km. The subset of the data analyzed along with the fitted bamlss model are provided in the FlashAustria data on R-Forge which can be installed by
install.packages("FlashAustria", repos = "http://R-Forge.R-project.org")
To model only the lightning counts with at least one lightning discharge we employ a negative binomial count distribution, truncated at zero. The data can be loaded as follows and the regression formula set up:
data("FlashAustria", package = "FlashAustria")
f <- list(
counts ~ s(d2m, bs = "ps") + s(q_prof_PC1, bs = "ps") +
s(cswc_prof_PC4, bs = "ps") + s(t_prof_PC1, bs = "ps") +
s(v_prof_PC2, bs = "ps") + s(sqrt_cape, bs = "ps"),
theta ~ s(sqrt_lsp, bs = "ps")
)
The expectation mu of the underlying untruncated negative binomial model is modeled by various smooth terms for the atmospheric variables while the overdispersion parameter theta only depends on one smooth regressor. To fit this challenging model, gradient boosting is employed in a first step to obtain initial values for the subsequent MCMC sampler. Running the model takes about 30 minutes on a well-equipped standard PC. In order to move quickly through the example we load the pre-computed model from the FlashAustria package:
data("FlashAustriaModel", package = "FlashAustria")
b <- FlashAustriaModel
But, of course, the model can also be refitted:
set.seed(111)
b <- bamlss(f, family = "ztnbinom", data = FlashAustriaTrain,
optimizer = boost, maxit = 1000, ## Boosting arguments.
thin = 5, burnin = 1000, n.iter = 6000) ## Sampler arguments.
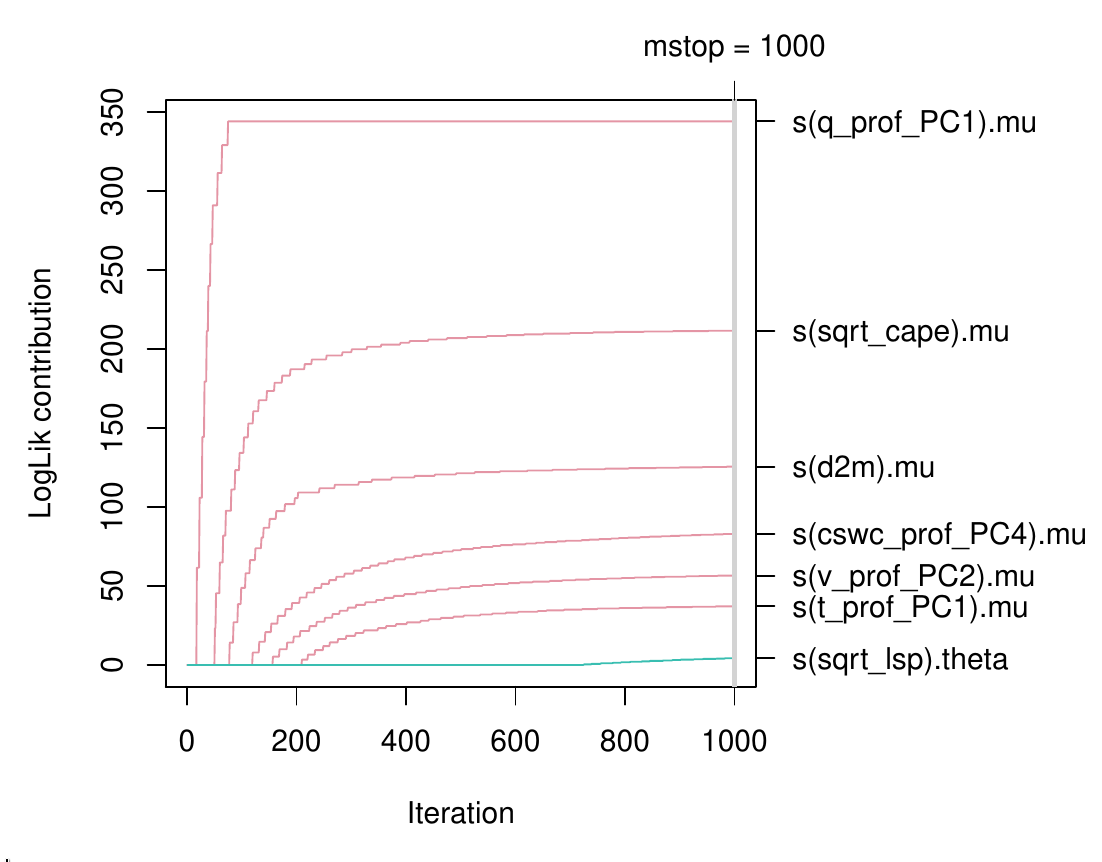
To explore this model in some more detail, we show a couple of visualizations. First, the contribution to the log-likelihood of individual terms during gradient boosting is depicted.
pathplot(b, which = "loglik.contrib", intercept = FALSE)
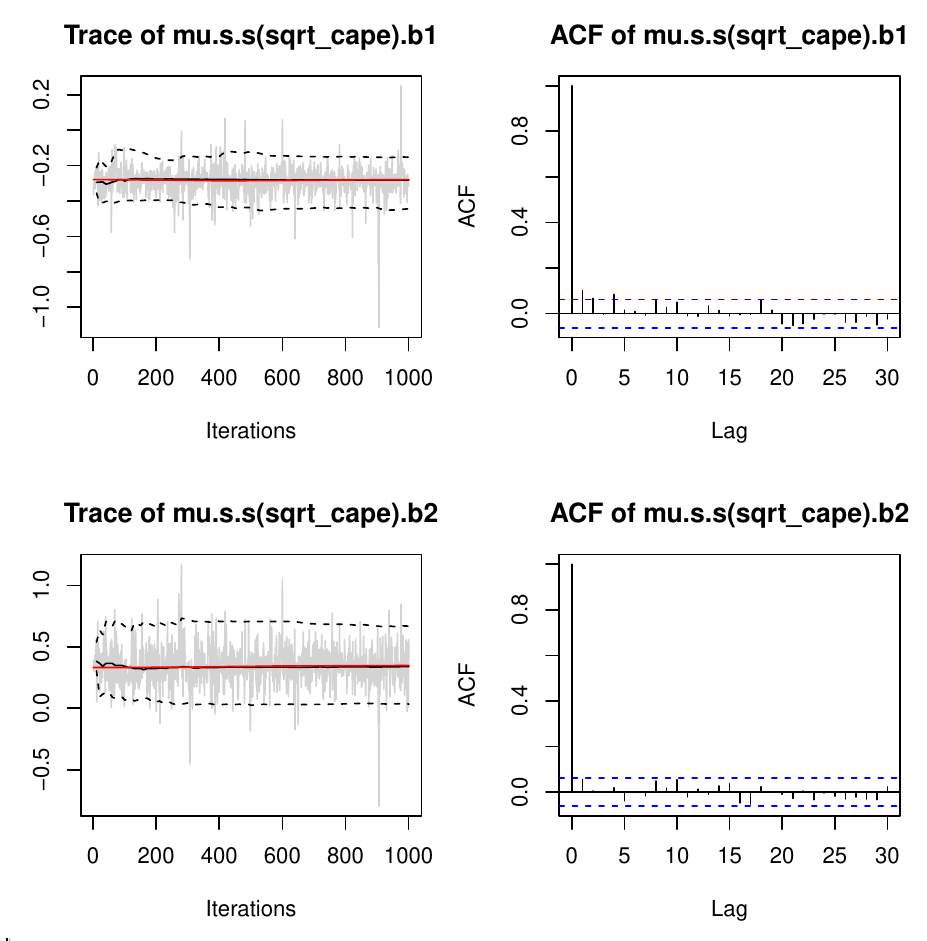
Subsequently, we show traceplots of the MCMC samples (left) along with autocorrelation for two splines the term s(sqrt_cape) of the model for mu.
plot(b, model = "mu", term = "s(sqrt_cape)", which = "samples")
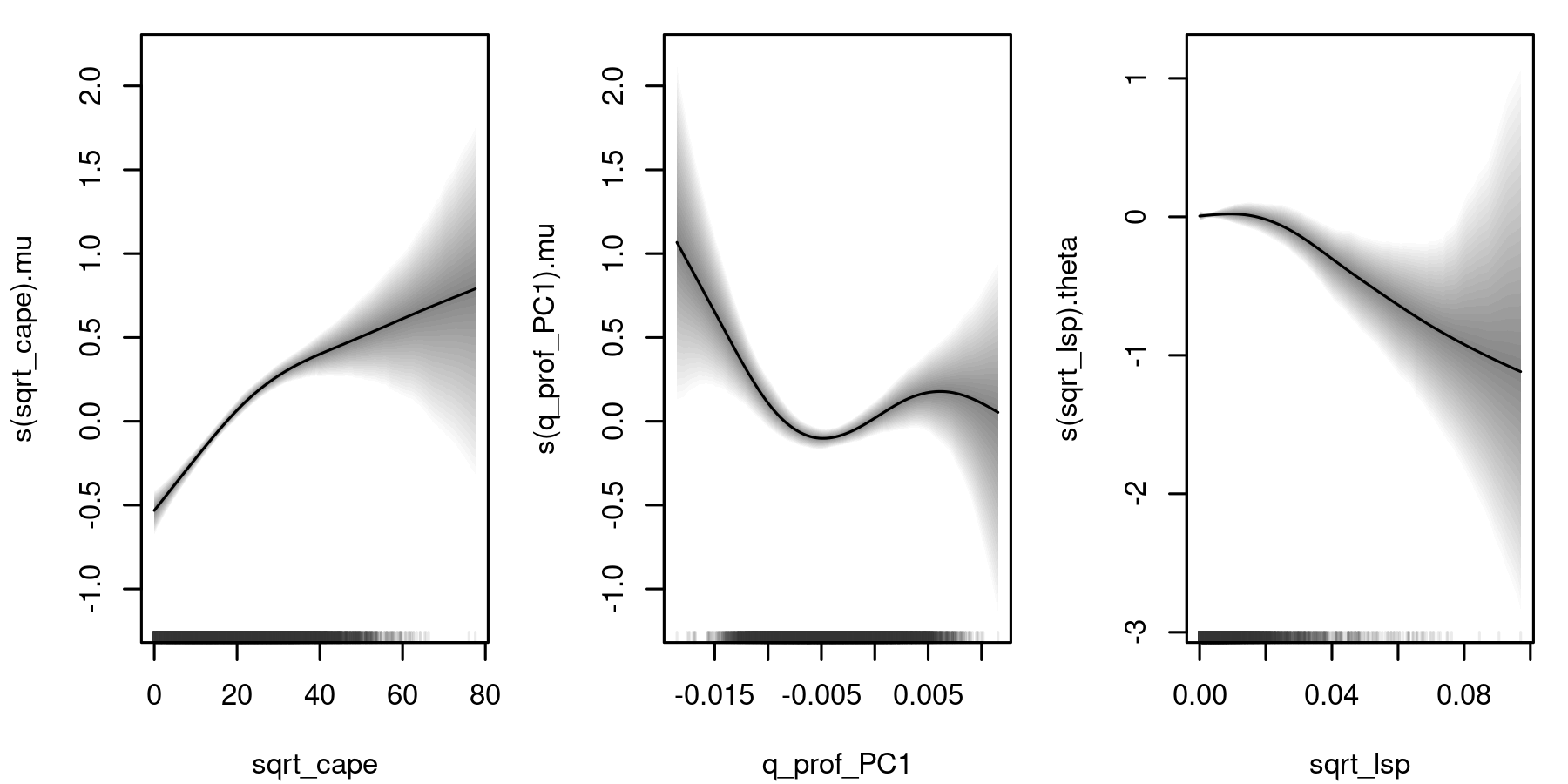
Next, the effects of the terms s(sqrt_cape) and s(q_prof_PC1) from the model for mu and term s(sqrt_lsp) from the model for theta are shown along with 95% credible intervals derived from the MCMC samples.
plot(b, term = c("s(sqrt_cape)", "s(q_prof_PC1)", "s(sqrt_lsp)"),
rug = TRUE, col.rug = "#39393919")
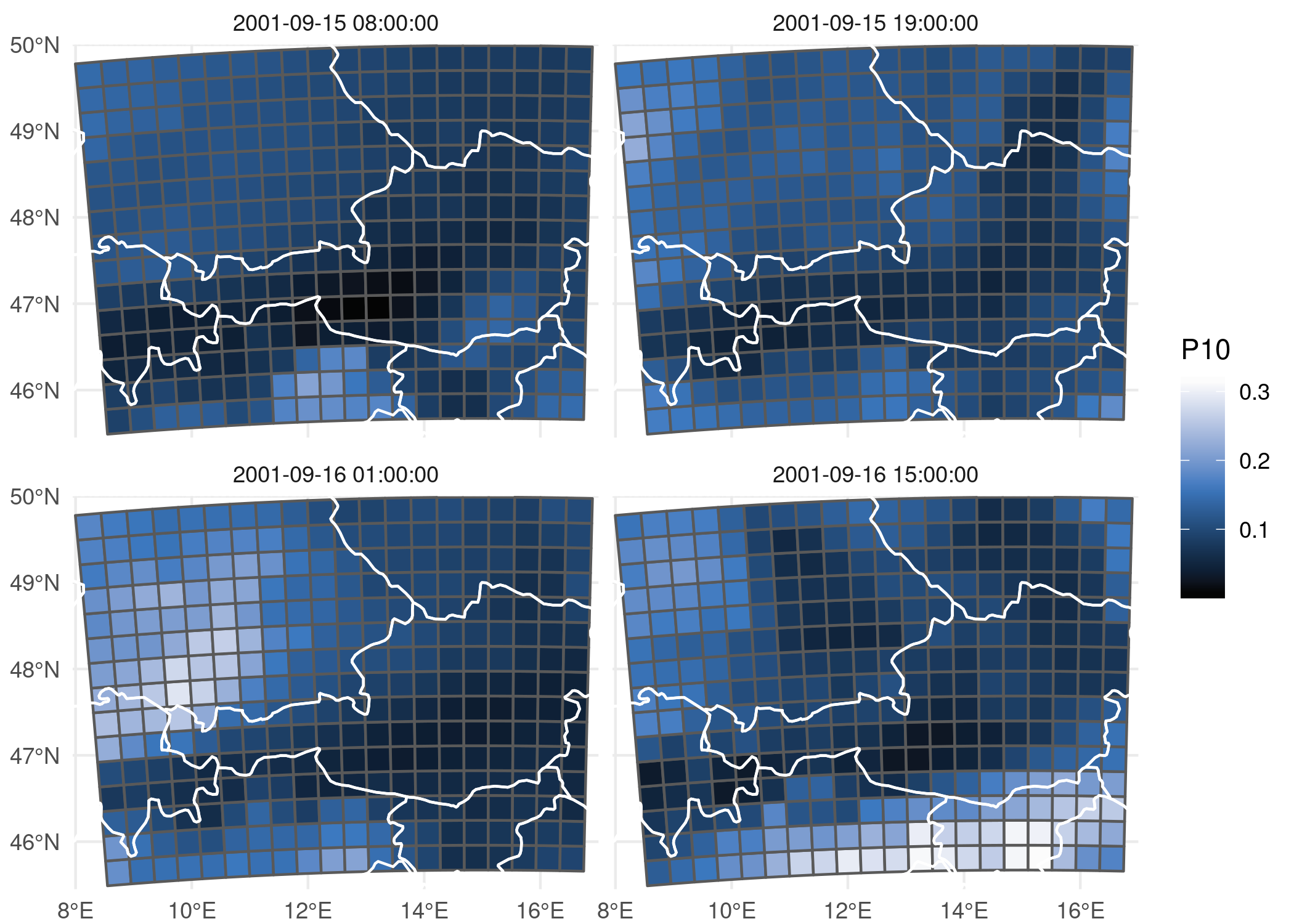
Finally, estimated probabilities for observing 10 or more lightning counts (within one grid box) are computed and visualized. The reconstructions for four time points on September 15-16, 2001 are shown.
fit <- predict(b, newdata = FlashAustriaCase, type = "parameter")
fam <- family(b)
FlashAustriaCase$P10 <- 1 - fam$p(9, fit)
world <- rnaturalearth::ne_countries(scale = "medium", returnclass = "sf")
library("ggplot2")
ggplot() + geom_sf(aes(fill = P10), data = FlashAustriaCase) +
colorspace::scale_fill_continuous_sequential("Oslo", rev = TRUE) +
geom_sf(data = world, col = "white", fill = NA) +
coord_sf(xlim = c(7.95, 17), ylim = c(45.45, 50), expand = FALSE) +
facet_wrap(~time, nrow = 2) + theme_minimal() +
theme(plot.margin = margin(t = 0, r = 0, b = 0, l = 0))