MPT trees published in BRM
Citation
Florian Wickelmaier, Achim Zeileis (2018). “Using Recursive Partitioning to Account for Parameter Heterogeneity in Multinomial Processing Tree Models.” Behavior Research Methods, 50(3), 1217-1233. doi:10.3758/s13428-017-0937-z
Abstract
In multinomial processing tree (MPT) models, individual differences between the participants in a study can lead to heterogeneity of the model parameters. While subject covariates may explain these differences, it is often unknown in advance how the parameters depend on the available covariates, that is, which variables play a role at all, interact, or have a nonlinear influence, etc. Therefore, a new approach for capturing parameter heterogeneity in MPT models is proposed based on the machine learning method MOB for model-based recursive partitioning. This procedure recursively partitions the covariate space, leading to an MPT tree with subgroups that are directly interpretable in terms of effects and interactions of the covariates. The pros and cons of MPT trees as a means of analyzing the effects of covariates in MPT model parameters are discussed based on simulation experiments as well as on two empirical applications from memory research. Software that implements MPT trees is provided via the mpttree function in the psychotree package in R.
Software
https://CRAN.R-project.org/package=psychotree
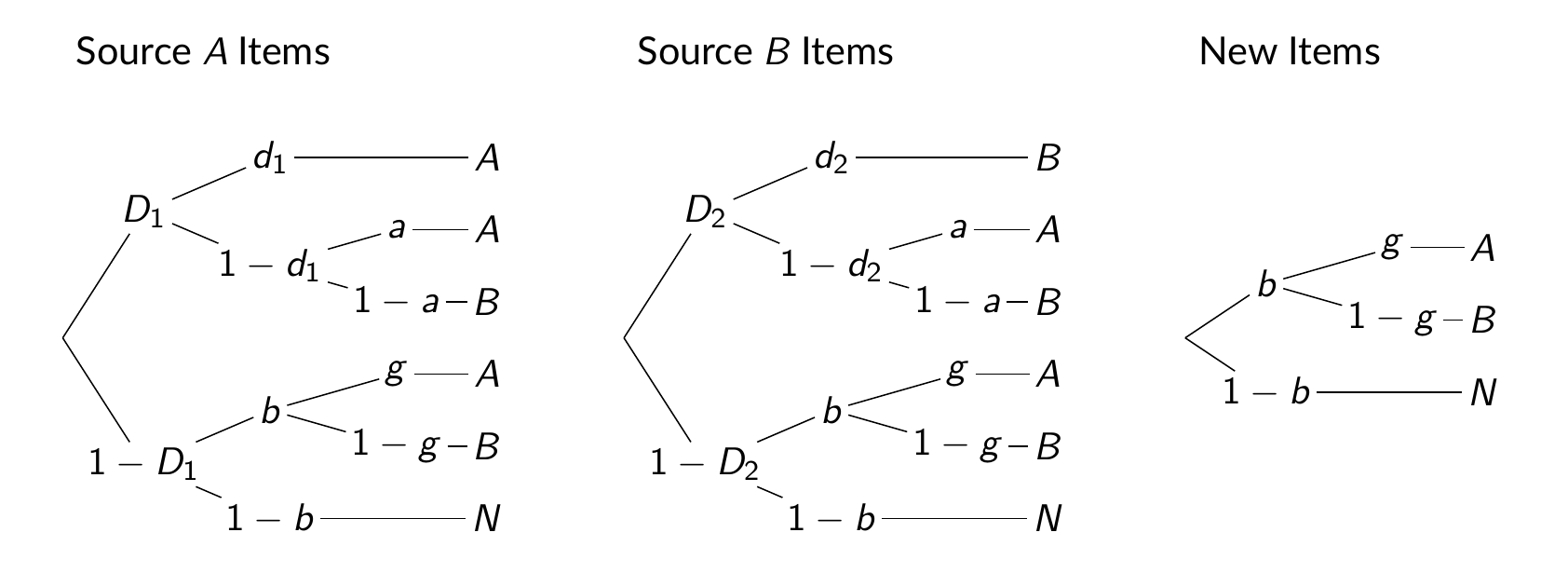
Illustration: Source monitoring
To highlight how MPT trees can capture the influence of covariates on the parameters in MPT models, data from a source monitoring experiment are analyzed, that was conducted at the Department of Psychology, University of Tübingen.
Study: Participants were presented with items from two different sources (labeled A vs. B) and afterwards, in a memory test, were shown old and new items intermixed and asked to classify them as either A, B, or new (N). In the experiment the two sources were controlled such that half of the respondents had to read the presented items either quietly (A = think) or aloud (B = say). The other half wrote them down (A = write) or read them aloud (B = say). Items were presented on a computer screen at a self-paced rate. In the final memory test, the studied items and distractor items had to be classified as either A, B, or new (N) by pressing a button on the screen.
Model: To infer the cognitive processes a well-known MPT model is employed that was established by the late Bill Batchelder (who passed away earlier this month) and David Riefer for the source monitoring paradigm:
Explanation: Consider the paths from the root to an A response for a Source A item (left). With probability D1, a respondent detects an item as old. If, in a second step, he/she is able to discriminate the item from a Source B item (d1), then the response will correctly be A; else, if discrimination fails (1 - d1), a correct A response can only be guessed with probability a. If the item was not detected as old in the first place (1 - D1), the response will be A only if there are both a response bias for “old” (b) and a guess for the item being Source A (g). The remaining paths in the left tree lead to classification errors (B, N). The trees for Source B and new items work analogously. Moreover, a = g is assumed for identifiability and discriminability is assumed to be equal for both sources (d1 = d2) as in a similar example in Batchelder and Riefer (1990).
Question: Do these probabilities in the source monitoring (D1, D2, d, b, g) depend on the source condition (think-say vs. write-say), or gender or age of the participants?
Answer: The MPT-based model tree (MOB) finds a highly significant difference between the think-say and write-say source condition. Furthermore, there is an age difference in the think-say condition that is significant at a Bonferroni-corrected 5% level. Gender is not found to play a significant role.
Probabilities: For the think-say sources (Nodes 3 and 4), probability D2 exceeds D1 indicating an advantage of say items over think items with respect to detectability. For the write-say sources (Node 5), D2 and D1 are about the same indicating that for these sources no such advantage exists. The think-say subgroup is further split by age with the older participants having lower values on D1 and d, which suggests lower detectability of think items and lower discriminability as compared to the younger participants. This age effect seems to depend on the type of sources as there is no such effect for the write-say sources. In addition, there are only small effects for the bias parameters b and g, which are psychologically less interesting. Some of the differences in the probabilities across groups/nodes can be brought out even more clearly by parameter estimates and corresponding 95% Wald confidence intervals: