Partially additive (generalized) linear model trees
Citation
Heidi Seibold, Torsten Hothorn, Achim Zeileis (2018). “Generalised Linear Model Trees with Global Additive Effects.” Advances in Data Analysis and Classification. Forthcoming. doi:10.1007/s11634-018-0342-1 arXiv
Abstract
Model-based trees are used to find subgroups in data which differ with respect to model parameters. In some applications it is natural to keep some parameters fixed globally for all observations while asking if and how other parameters vary across subgroups. Existing implementations of model-based trees can only deal with the scenario where all parameters depend on the subgroups. We propose partially additive linear model trees (PALM trees) as an extension of (generalised) linear model trees (LM and GLM trees, respectively), in which the model parameters are specified a priori to be estimated either globally from all observations or locally from the observations within the subgroups determined by the tree. Simulations show that the method has high power for detecting subgroups in the presence of global effects and reliably recovers the true parameters. Furthermore, treatment-subgroup differences are detected in an empirical application of the method to data from a mathematics exam: the PALM tree is able to detect a small subgroup of students that had a disadvantage in an exam with two versions while adjusting for overall ability effects.
Software
https://CRAN.R-project.org/package=palmtree
Illustration: Treatment differences in mathematics exam
PALM trees are employed to investigate treatment differences in a mathematics 101 exam (for first-year business and economics students) at Universität Innsbruck. Due to limited availability of seats in the exam room, students could self-select into one of two exam tracks that were conducted back to back with slightly different questions on the same topics. The question is whether this “treatment” of splitting the students into two tracks was fair in the sense that it is on average equally difficult for the two groups. To investigate the question the data are loaded from the psychotools package, points are scaled to achieved percent in [0, 100], and the subset of variables for the analysis are selected:
data("MathExam14W", package = "psychotools")
MathExam14W$tests <- 100 * MathExam14W$tests/26
MathExam14W$pcorrect <- 100 * MathExam14W$nsolved/13
MathExam <- MathExam14W[ , c("pcorrect", "group", "tests", "study",
"attempt", "semester", "gender")]
A naive check could be whether the percentage of correct points (pcorrect) differs between the two groups:
ci <- function(object) cbind("Coefficient" = coef(object), confint(object))
ci(lm(pcorrect ~ group, data = MathExam))
## Coefficient 2.5 % 97.5 %
## (Intercept) 57.60 55.1 60.08
## group2 -2.33 -5.7 1.03
This shows that the second group achieved on average 2.33 percentage points less than the first group. But the corresponding confidence interval conveys that this difference is not significant.
However, it is conceivable that stronger (or weaker) students selected themselves more into one of the two groups. And if the assignment had been random, then the “treatment effect” might have been larger or even smaller. Luckily, an independent measure of the students’ ability is available, namely the percentage of points achieved in the online tests conducted during the semester prior to the exam. Adjusting for that increases the treatment effect to a decrease of 4.37 percentage points which is still non-significant, though. This is due to weaker students self-selecting into the second group. Moreover, the tests coefficient signals that 1 more percentage point from the online tests lead on average to 0.855 more percentage points in the written exam.
ci(lm(pcorrect ~ group + tests, data = MathExam))
## Coefficient 2.5 % 97.5 %
## (Intercept) -5.846 -13.521 1.828
## group2 -4.366 -7.231 -1.502
## tests 0.855 0.756 0.955
Finally, PALM trees are used to assess whether there are subgroups of differential group treatment effects when adjusting for a global additive tests effect. Potential subgroups can be formed from the covariates tests, type of study (three-year bachelor vs. four-year diploma), the number of times the students attempted the exam, number of semesters, and gender. Using palmtree this can be easily carried out:
library("palmtree")
palmtree_math <- palmtree(pcorrect ~ group | tests | tests +
study + attempt + semester + gender, data = MathExam)
print(palmtree_math)
## Partially additive linear model tree
##
## Model formula:
## pcorrect ~ group | tests + study + attempt + semester + gender
##
## Fitted party:
## [1] root
## | [2] attempt <= 1
## | | [3] tests <= 92.3: n = 352
## | | (Intercept) group2
## | | -7.09 -3.00
## | | [4] tests > 92.3: n = 79
## | | (Intercept) group2
## | | 14.0 -14.5
## | [5] attempt > 1: n = 298
## | (Intercept) group2
## | 2.33 -1.70
##
## Number of inner nodes: 2
## Number of terminal nodes: 3
## Number of parameters per node: 2
## Objective function (residual sum of squares): 253218
##
## Linear fixed effects (from palm model):
## tests
## 0.787
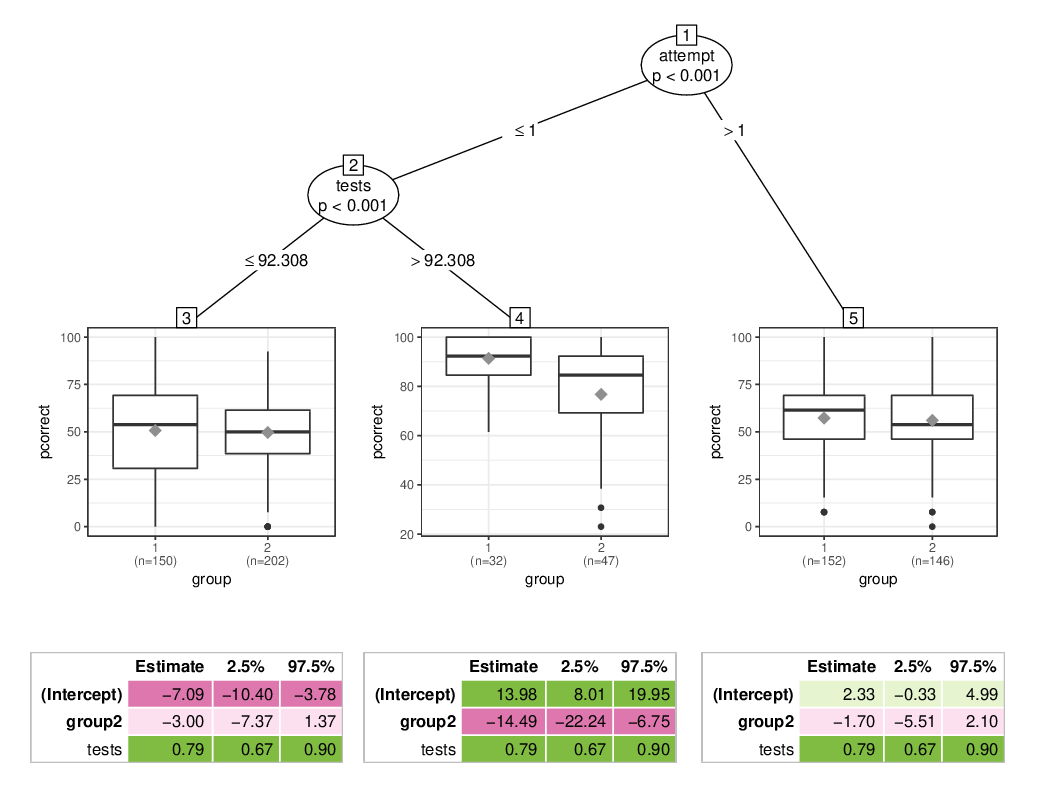
A somewhat enhanced version of plot(palmtree_math) is shown below:
This indicates that for most students the group treatment effect is indeed negligible. However, for the subgroup of “good” students (with high percentage correct in the online tests) in the first attempt, the exam in the second group was indeed more difficult. On average the students in the second group obtained -14.5 percentage points less than in the first group.
ci(palmtree_math$palm)
## Coefficient 2.5 % 97.5 %
## (Intercept) -7.088 -16.148 1.971
## .tree4 21.069 13.348 28.791
## .tree5 9.421 5.168 13.673
## tests 0.787 0.671 0.903
## .tree3:group2 -2.997 -6.971 0.976
## .tree4:group2 -14.494 -22.921 -6.068
## .tree5:group2 -1.704 -5.965 2.557
The absolute size of this group difference is still moderate, though, corresponding to about half an exercise out of 13.
Simulation study
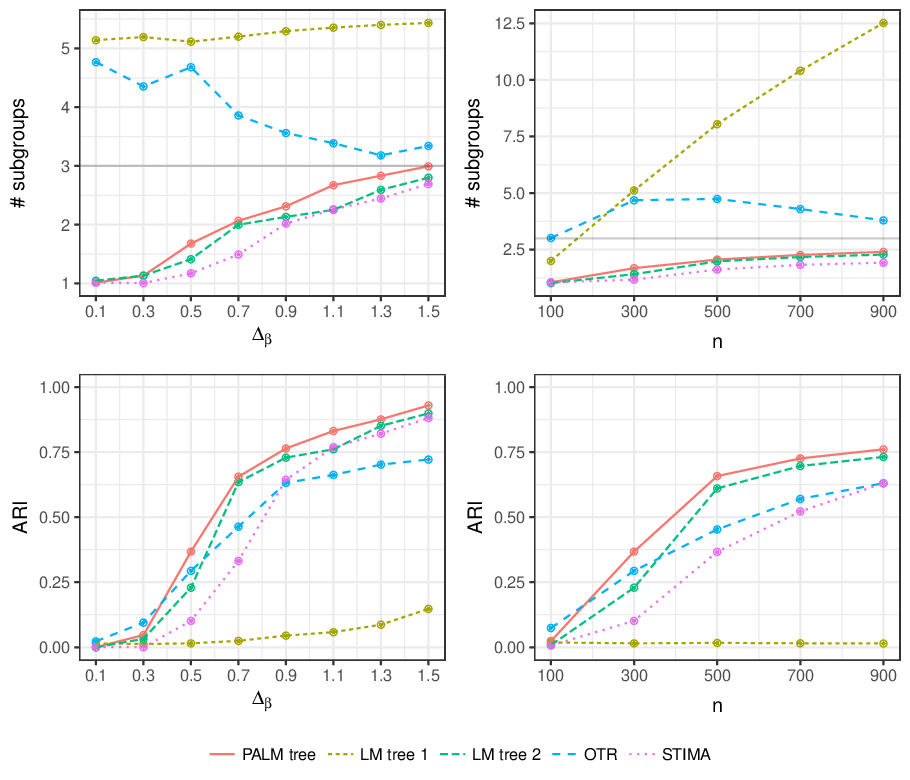
In addition to the empirical case study the manuscript also provides an extensive simulation study comparing the performance of PALM trees in treatment-subgroup scenarios to standard linear model (LM) trees, optimal treatment regime (OTR) trees (following Zhang et al. 2012), and the STIMA algorithm (simultaneous threshold interaction modeling algorithm). The study evaluates the methods with respect to (1) finding the correct subgroups, (2) not splitting when there are no subgroups, (3) finding the optimal treatment regime, and (4) correctly estimating the treatment effect.
Here we just briefly highlight the results for question (1): Are the correct subgroups found? The figure below shows the mean number of subgroups (over 150 simulated data sets and mean adjusted rand index (ARI) for increasing treatment effect differences Δβ and number of observations n.
This shows that PALM trees perform increasingly well and somewhat better with respect to these metrics than the competitors. More details on the different scenarios and corresponding evaluations can be found in the manuscript. More replication materials are provided along with the manuscript on the publisher’s web page.