Clustered covariances in sandwich 2.5-0
Enhancements in version 2.5-0
Most of the improvements and new features pertain to clustered covariances which had been introduced to the sandwich package last year in version 2.4-0. For this my PhD student Susanne Berger and myself (= Achim Zeileis) teamed up with Nathaniel Graham, the maintainer of the multiwayvcov package. With the new version 2.5-0 almost all features from multiwayvcov have been ported to sandwich, mostly implemented from scratch along with generalizations, extensions, speed-ups, etc.
The full list of changes can be seen in the NEWS file. The most important changes are:
-
The manuscript
vignette("sandwich-CL", package = "sandwich")has been significantly improved based on very helpful and constructive reviewer feedback. See also below. -
The
clusterargument for thevcov*()functions can now be a formula, simplifying its usage (see below).NAhandling has been added as well. -
Clustered bootstrap covariances have been reimplemented and extended in
vcovBS(). A dedicated method forlmobjects is considerably faster now and also includes various wild bootstraps. -
Convenient parallelization for bootstrap covariances is now available.
-
Bugs reported by James Pustejovsky and Brian Tsay, respectively, have been fixed.
Manuscript/vignette
Susanne Berger, Nathaniel Graham, Achim Zeileis: Various Versatile Variances: An Object-Oriented Implementation of Clustered Covariances in R
Clustered covariances or clustered standard errors are very widely used to account for correlated or clustered data, especially in economics, political sciences, or other social sciences. They are employed to adjust the inference following estimation of a standard least-squares regression or generalized linear model estimated by maximum likelihood. Although many publications just refer to “the” clustered standard errors, there is a surprisingly wide variety of clustered covariances, particularly due to different flavors of bias corrections. Furthermore, while the linear regression model is certainly the most important application case, the same strategies can be employed in more general models (e.g. for zero-inflated, censored, or limited responses).
In R, functions for covariances in clustered or panel models have been somewhat scattered or available only for certain modeling functions, notably the (generalized) linear regression model. In contrast, an object-oriented approach to “robust” covariance matrix estimation - applicable beyond lm() and glm() - is available in the sandwich package but has been limited to the case of cross-section or time series data. Now, this shortcoming has been corrected in sandwich (starting from version 2.4.0): Based on methods for two generic functions (estfun() and bread()), clustered and panel covariances are now provided in vcovCL(), vcovPL(), and vcovPC(). Moreover, clustered bootstrap covariances, based on update() for models on bootstrap samples of the data, are provided in vcovBS(). These are directly applicable to models from many packages, e.g., including MASS, pscl, countreg, betareg, among others. Some empirical illustrations are provided as well as an assessment of the methods’ performance in a simulation study.
Illustrations
To show how easily the clustered covariances from sandwich can be applied in practice, two short illustrations from the manuscript/vignette are used. In addition to the sandwich package the lmtest package is employed to easily obtain Wald tests of all coefficients:
library("sandwich")
library("lmtest")
options(digits = 4)
First, a Poisson model with clustered standard errors from Aghion et al. (2013, American Economic Review) is replicated. To investigate the effect of institutional ownership on innovation (as captured by citation-weighted patent counts) they employ a (pseudo-)Poisson model with industry/year fixed effects and standard errors clustered by company, see their Table I(3):
data("InstInnovation", package = "sandwich")
ii <- glm(cites ~ institutions + log(capital/employment) + log(sales) + industry + year,
data = InstInnovation, family = poisson)
coeftest(ii, vcov = vcovCL, cluster = ~ company)[2:4, ]
## Estimate Std. Error z value Pr(>|z|)
## institutions 0.009687 0.002406 4.026 5.682e-05
## log(capital/employment) 0.482884 0.135953 3.552 3.826e-04
## log(sales) 0.820318 0.041523 19.756 7.187e-87
Second, a simple linear regression model with double-clustered standard errors is replicated using the well-known Petersen data from Petersen (2009, Review of Financial Studies):
data("PetersenCL", package = "sandwich")
p <- lm(y ~ x, data = PetersenCL)
coeftest(p, vcov = vcovCL, cluster = ~ firm + year)
## t test of coefficients:
##
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 0.0297 0.0651 0.46 0.65
## x 1.0348 0.0536 19.32 <2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Simulation
In addition to the description of the methods and the software, the manuscript/vignette also contains a simulation study that investigates the properties of clustered covariances. In particular, this assesses how well the methods perfom in models beyond linear regression but also compares different types of bias adjustments (HC0-HC3) and alternative estimation techniques (generalized estimating equations, mixed effects).
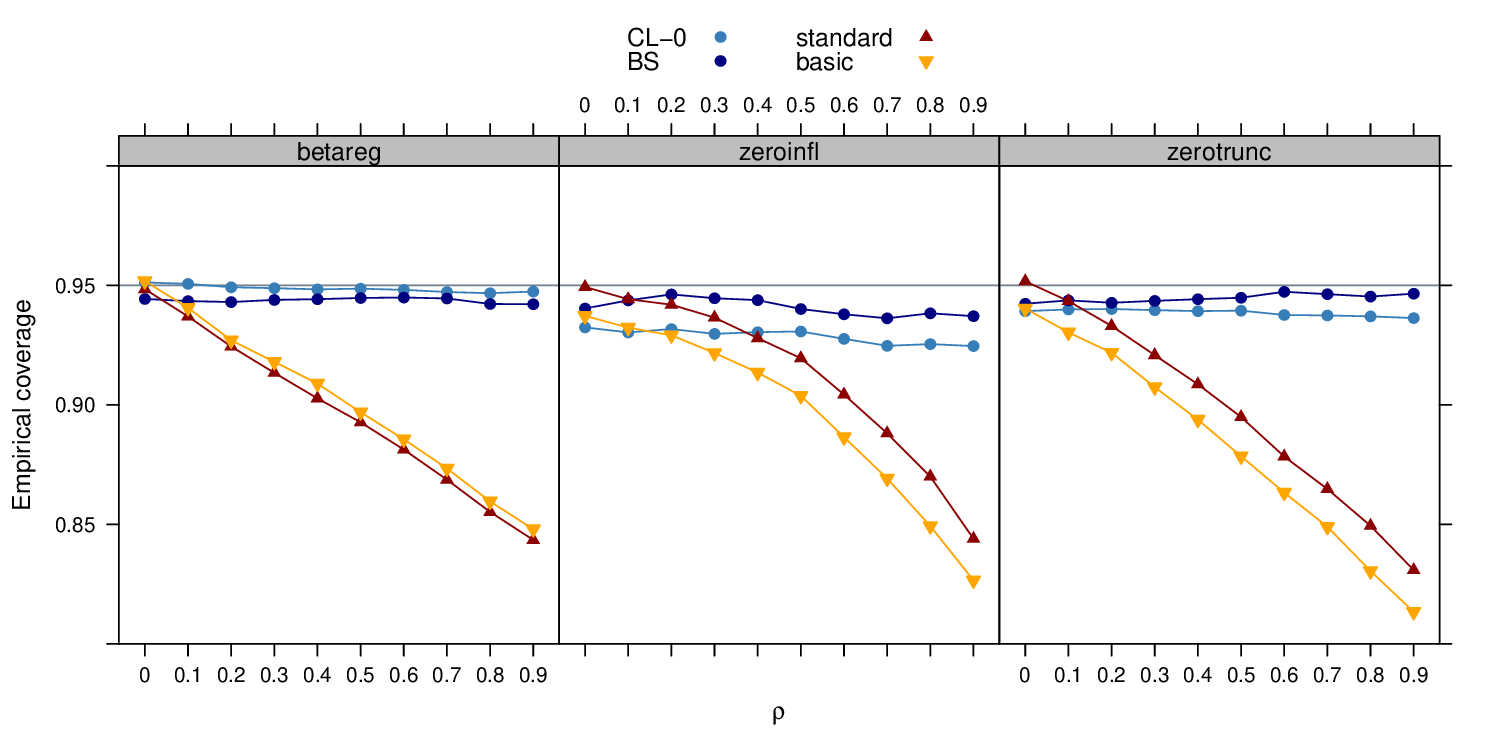
The detailed results are presented in the manuscript - here we just show the results from one of the simulation experiments: The empirical coverage of 95% Wald confidence intervals is depicted for a beta regression, zero-inflated Poisson, and zero-truncated Poisson model. With increasing correlation within the clusters the conventional “standard” errors and “basic” robust sandwich standard errors become too small thus leading to a drop in empirical coverage. However, both clustered HC0 standard errors (CL-0) and clustered bootstrap standard errors (BS) perform reasonably well, leading to empirical coverages close to the nominal 0.95.
Details: Data sets were simulated with 100 clusters of 5 observations each. The cluster correlation (on the x-axis) was generated with a Gaussian copula. The only regressor had a correlation of 0.25 with the clustering variable. Empirical coverages were computed from 10,000 replications.